Estimation of the motion parameters of a platform

Contents 1 Linear motion speed 2 Wheel rotation speed 3 Motion modes 3.1 Linear motion 3.1.1 Longitudinal mode 3.1.2 Lateral mode 3.2 Rotation 3.3 Spline follow mode (Incorrect)

Linear motion speed

The diameter of a platform wheel is D=140 mm. The length of wheel circumference is L=π·D=439.81mm. The maximal motor speed is w_motor=5200 rpm. The gear ratio is q=100:1. The maximal output shaft speed of a gearbox, which is also a wheel speed is w_shaft=w_motor/q=5200/100=52 rpm = 52/60 rotations/sec. The path S, which wheel can move for one second is equal S=w_shaft*L = 381.1688 mm = 0.38116 meters. Velocity is S/t (t = 1 second), V = 0.38116 m/s = 1.37216 km/h.

• Maximal linear speed: V = 0.38116 m/s

Wheel rotation speed

The same motor system with rotation speed w_shaft is rotating each wheel. Hence, the maximal rotation speed is w_shaft*2*π = 5.445427 rad/second = 312°/second.

• Maximal rotation speed: w_shaft = 5.445427 rad/s = 312°/s.

In normal conditions a single wheel will not change direction on more than [-45°,+90°], hence the maximal rotation degree is 90-(-45)= 135°. Hence, maximal time required for each wheel position is (135/312) seconds = 0.433 s.

• Wheel positioning time: T_pos ≤ 0.433 s (at maximal motor speed).

Motion modes

Linear motion

Longitudinal mode

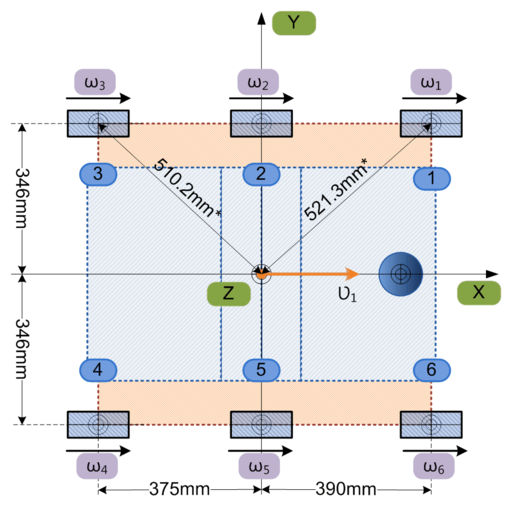
Below is the illustration of the straight (longitudinal, forward and backward) motion process. Top view:

Lateral mode

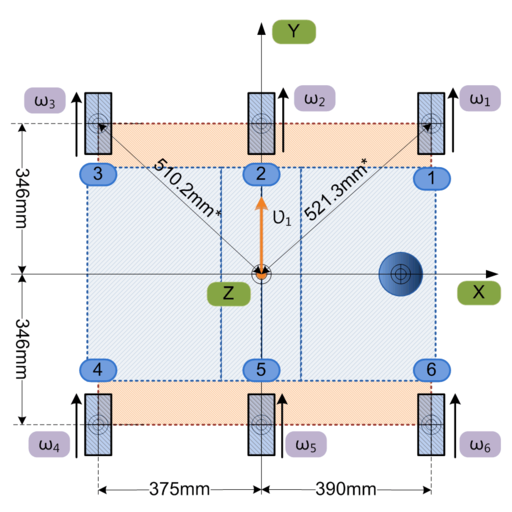
Below is the illustration of the lateral motion process. Top view:

Rotation

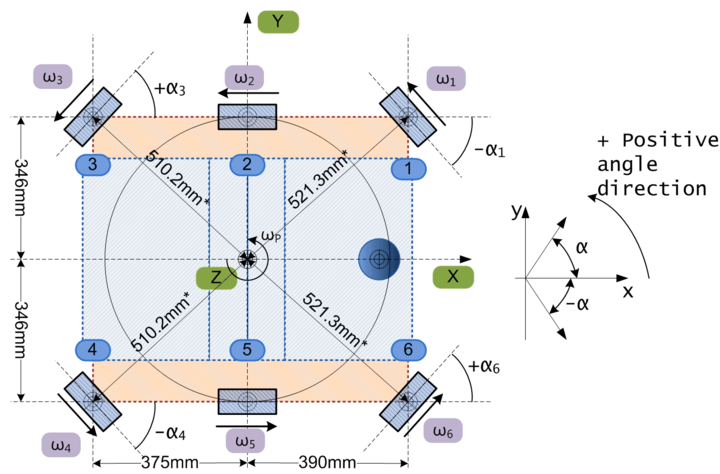
Below is the illustration of the platform rotation process. Top view:

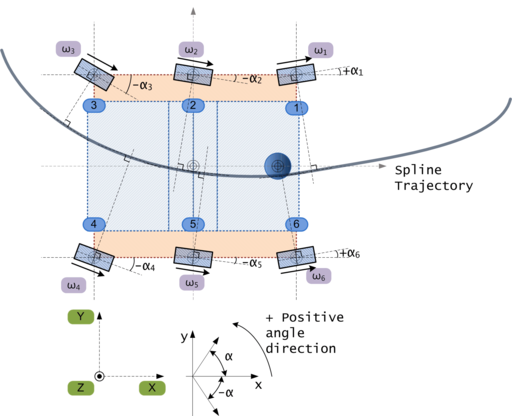
Spline follow mode (Incorrect)

Todo: This design is incorrect! For history only.

Below is the illustration of how a spline trajectory can be followed. Top view: